external potential

Choosing external potential is one of the most important parameters. Here are the list of already implemeted external potentials. In the future we plan to implement a function in which one could customize external potential.

iext=70

This type of external potential is used for two body static calculations. It prevents nuclei to gain distance - due to Coulomb repulsion. Dropdowns at the edges are for the

Code

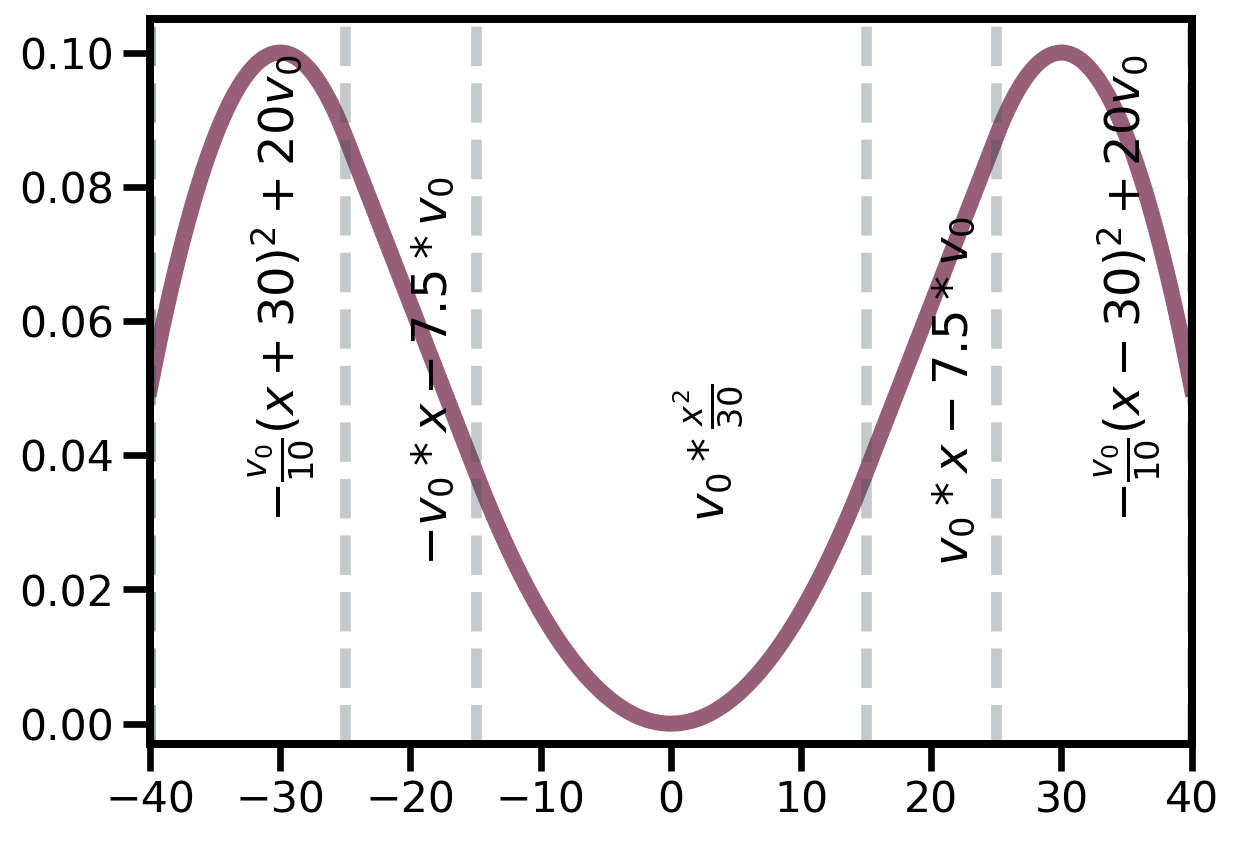
import numpy as np
import matplotlib.pyplot as plt

iext = 70
v0 = 0.005

X = np.linspace(-40, 40, 2000)
Y = []

graphite = '#3C4C4C'

if iext == 70:
    for x in X:
        if (x < -25.0):
            Y.append(-v0 / 10.0 * (x + 30.0)**2 + 20 * v0)
        elif (x < -15.0):
            Y.append(-v0 * x - 7.5 * v0)
        elif (x < 15.0):
            Y.append(v0 * x**2 / 30.0)
        elif (x < 25.0):
            Y.append(v0 * x - 7.5 * v0)
        else:
            Y.append(-v0 / 10.0 * (x - 30.0)**2 + 20 * v0)

    fig, ax = plt.subplots()

    ax.plot(X, Y, c='#965F77', linewidth=6)

    ax.set_ylim([-.003, 1.05*max((-v0 / 10.0 * (X + 30.0)**2 + 20 * v0))])
    ymax = max((-v0 / 10.0 * (X + 30.0)**2 + 20 * v0))
    # -40 -> -25 range
    x1 = min(X) - (min(X) + 25) / 2
    ax.axvline(x=min(X), linestyle='dashed',
               color=graphite, linewidth=4, alpha=0.3)
    ax.text(x=x1, y=ymax/3,
            s=r'$-\frac{v_0}{10} \left(x + 30\right)^2 + 20 v_0$', rotation=90, size=18)

    # -25 -> -15 range
    x2 = (-25 - 15) / 2
    ax.axvline(x=-25, linestyle='dashed',
               color=graphite, linewidth=4, alpha=0.3)
    ax.text(x=x2, y=ymax/4, s=r'$-v_0 * x - 7.5 * v_0$', rotation=90, size=18)

    # -15 -> +15 range
    x3 = 0
    ax.axvline(x=-15, linestyle='dashed',
               color=graphite, linewidth=4, alpha=0.3)
    ax.text(x=x3, y=ymax/3, s=r'$v_0 * \frac{x^2}{30}$', rotation=90, size=18)
    ax.axvline(x=15, linestyle='dashed',
               color=graphite, linewidth=4, alpha=0.3)

    # 15 -> 25 range
    x4 = (25 + 15) / 2
    ax.axvline(x=25, linestyle='dashed',
               color=graphite, linewidth=4, alpha=0.3)
    ax.text(x=x4, y=ymax/4, s=r'$v_0 * x - 7.5 * v_0$', rotation=90, size=18)

    # 25 -> 40 range
    x5 = max(X) - (max(X) - 25) / 2
    ax.axvline(x=min(X), linestyle='dashed',
               color=graphite, linewidth=4, alpha=0.3)
    ax.text(x=x5, y=ymax/3,
            s=r'$-\frac{v_0}{10} \left(x - 30\right)^2 + 20 v_0$', rotation=90, size=18)
    ax.axvline(x=max(X), linestyle='dashed',
               color=graphite, linewidth=4, alpha=0.3)

    for axis in ['top', 'bottom', 'left', 'right']:
        ax.spines[axis].set_linewidth(3)
    ax.tick_params(length=10, width=2.5)
    
    ax.set_xlim(-40,40)
    
    for label in (ax.get_xticklabels() + ax.get_yticklabels()):
        label.set_fontsize(16)

    plt.show()

Figure 1: An external potential iext=70

In the code it is done by the folowing loop:

for (i = 0; i < nxyz; i++)
{
  double z = lattice_coords->za[i];

  if (z < -25.0)
    v_ext[i] = -v0 / 10.0 * pow((z + 30.0), 2.0) + 20 * v0;
  else if (z < -15.0)
    v_ext[i] = -v0 * z - 7.5 * v0;
  else if (z < 15.0)
    v_ext[i] = v0 * z * z / 2.0 / 15.0;
  else if (z < 25.0)
    v_ext[i] = v0 * z - 7.5 * v0;
  else
    v_ext[i] = -v0 / 10.0 * pow((z - 30.0), 2.0) + 20 * v0;
}

where parameter v0 is adjusted by the user using the following formula (in the future it will be changed to be automatically set):

v_0 = \frac{e^2 Z_L Z_R}{2000 d}

where e^2= (\hbar c)\alpha \approx 1.44, Z is a number of protons in _L left and _R right nuclei, d is a center of mass distance between the nuclei